8. Mundell-Fleming Model with a
Floating Exchange Rate
(No handout; chapter 13)
What is the Mundell-Fleming model?
In an open economy with external trade and financial transactions, how are
the key macro variables (GDP, inflation, balance of payments, exchange rates,
interest rates, etc) determined and interact with each other? What are the effects of fiscal
and monetary policies? The Mundell-Fleming model is the standard open
macroeconomic model that tries to answer these questions. Most open macroeconomy
models in the textbooks are variations of the Mundell-Fleming model.
Theoretically, it is the most popular model. But its
applicability to actual policy making is not as high as we would hope
(especially for developing and transition countries). Blind
application of this model to your country may not yield good results,
because the model is based on many assumptions which may be unrealistic. But this is the best model that economists have. So use it
carefully.
 In
1963 when he was young, Prof.
Robert Mundell (photo) was working with Marcus Fleming at the IMF and
wrote a paper which gave birth to this model. He has been at Columbia University
(New York) in the last 25 years. He has been a strong advocate of stabilization of
major currencies and establishment of euro. In 1999, he won the Nobel Prize
in economics, partly because of the Mundell-Fleming model.
In
1963 when he was young, Prof.
Robert Mundell (photo) was working with Marcus Fleming at the IMF and
wrote a paper which gave birth to this model. He has been at Columbia University
(New York) in the last 25 years. He has been a strong advocate of stabilization of
major currencies and establishment of euro. In 1999, he won the Nobel Prize
in economics, partly because of the Mundell-Fleming model.
The Mundell-Fleming model is an open macro application of the standard
IS-LM analysis. More precisely, it is an IS-LM analysis with trade and
international capital mobility. (If you do not know what the IS-LM model is,
you have a problem. Please look at any intermediate macroeconomic textbook
or ask your friend).
Consider the following three aspects of the macroeconomy:
(1) Aggregate demand (IS and LM curves, representing goods and money
markets)
(2) Aggregate supply (production function and labor market)
(3) Balance of payments (current account and capital account)
The usual textbook exposition (with no trade or capital mobility)
combines (1) and (2), with a
downward sloping AD (aggregate demand) curve and an upward-sloping AS (aggregate supply) curve.
The Mundell-Fleming model combines (1) and (3), namely AD and B (balance
of payments) curves. This means that the Mundell-Fleming model (in its simplest version) has no supply side constraint. As in the most
elementary
Keynesian model, it implicitly assumes that capital and labor are generally
underemployed so that any demand stimulus will expand real GDP (rather than
cause inflation).
Let us now look at the construction of the AD curve and B curve below. (I
will basically use the notation of Rivera-Batiz' book but may add a few more
symbols).
Aggregate demand - IS curve
Aggregate demand is composed of two parts: absorption (A, namely, domestic
demand) and trade balance (T, namely, foreign demand). We ignore service trade,
factor income and transfers, so the current account is the same as the trade
balance.
Y = A +
T
(GDP by expenditure decomposition)
where
A = C + I + G (definition
of absorption)
= A (Y, i; G)
A1
>0, A2 <0, A3 >0; G is
an exogenous spending (shift parameter)
[A1 means partial derivative of A with respect to first variable,
etc]
and
T = M* - qM
(definition of trade balance, measured in domestic currency)
= T (q, Y*,
Y) T1 >0, T2
>0, T3 <0; foreign income Y* is
assumed fixed
(Y: income C: private consumption I: private investment
G: government spending M: imports M*: foreign imports (=our
exports), i: interest rate)
Note that A and T are defined as real variables (deflated by
domestic price P). The real exchange rate q is defined thus:
q = EP*/P
(a rise in q means real depreciation of home currency)
Please note that T1 >0, namely, partial derivative of trade balance
with respect to q is positive. This means that the Marshall-Lerner
condition is satisfied, so real depreciation will improve the trade balance
(when other variables remain unchanged).
From above, we have
Y = A (Y, i; G) + T (q, Y*,
Y)
= F (Y, i, q;
G)
Note: 0 < F1 < 1 [can you explain why?]
Collecting Y to the left-hand side,
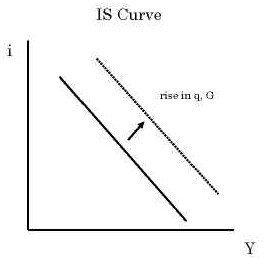
Y = f (i, q; G)
f1
<0, f2 >0, f3 >0
This is our IS curve. It is downward-sloping in the (i, Y) plane. Moreover, a
rise in q (real depreciation) or a rise in G (government spending) shifts the IS
curve up and to the right.
Aggregate demand - LM curve
The LM curve is the same as in the domestic macro version. It shows the
condition for money market equilibrium.
In particular, we ignore the possibility of "currency
substitution," a phenomenon where domestic citizens hold foreign
currency (typically US dollar) as well as domestic currency, and change
their relative shares as circumstances change. No currency substitution is a reasonable
assumption in developed countries, where people hold only domestic currency.
But in many developing countries, currency substitution may be a big factor
that influences the money demand.
Currency substitution is also called
"dollarization." But dollarization has two meanings: (1) the
situation where people use dollars in addition to domestic currency,
because they do not trust the latter (in this case, the monetary authority
usually tries to prevent the use of dollar); (2) the situation where the
government declares that the national currency is the US dollar, abolishes the
central bank, and gives up independent monetary policy. Currency
substitution is equivalent to the first (traditional) meaning of dollarization.
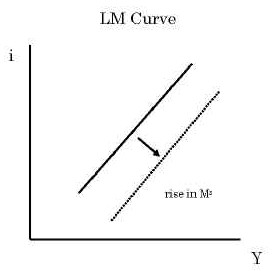
The LM curve is simply:
Ms/P = LD (i,
Y) LD1
<0, LD2 >0
(Ms: money supply P: price level)
As in the domestic version, it is upward-sloping in the (i, Y) plane. A
rise in money supply Ms shifts the LM curve down and to the
right. In this formulation, the price level P is assumed fixed. This may be
unrealistic in a small open economy where exchange rate pass-through (E
-> P) is significant.
Balance of payments
The balance of payments (B) is the sum of current account (T) and capital
account (K). Remember, for simplicity we have assumed away the flows of
service, factor income and transfers so that the current account is
identical with the trade balance.
B = T + K
= T (q, Y) + K (i - i*)
T1 >0, T2 <0; K1
> 0
= 0
Here, we assume the following:
--The exchange rate is floating (the real exchange rate q is also
flexible).
--The monetary authority does not intervene in the foreign exchange
market. This means that there is no change in international reserves,
the monetary account is zero, and therefore the current account and the
capital account must always add up to zero (T + K = 0).
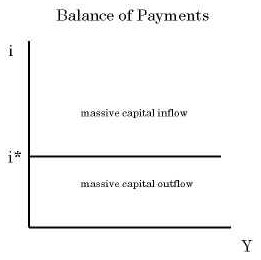
--Additionally, we assume perfect capital mobility. This means
that i = i*, K1 = +∞, and K is indeterminate. In other words, if i > i* there
will be a massive capital inflow into the home country and if i < i*
there will be a massive outflow, so the only way K can remain
finite is when i = i*. When that happens, K can take
any value (positive or negative) to offset T, so that T + K = 0 holds.
--The exchange rate expectation is static. That is to say,
people expect that the future exchange rate will be the same as today's (even
though the exchange rate is floating). This is a simplifying assumption.
Thus, instead of the usual uncovered interest parity (i = i* + x, see lecture
4), we have i = i* (because x = 0).
If we depict this situation in the (i, Y) plane, we have a horizontal
line at i*. The domestic interest rate must be equal to the world interest
rate. There will be a massive capital inflow above that line, and a
massive capital outflow below that line.
Equilibrium
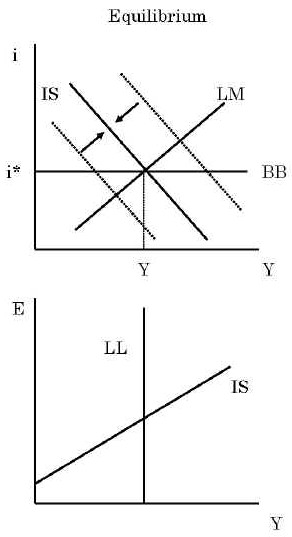
Under a freely floating exchange rate and perfect capital mobility, the
following three equations derived above determine the equilibrium position.
Y = f (i, q; G)
f1
<0, f2 >0, f3
>0
<IS>
Ms/P = LD (i,
Y) LD1
<0, LD2
>0 <LM>
i = i*
<BOP>
Recall that foreign income, foreign interest rate and domestic price are
all fixed (Y*, i*,
P).
The equilibrium can be pictured as follows:
Comparative statics
Comparative statics means checking how the equilibrium changes if
one input variable is changed. More technically, it is a matrix of signs (+
or -) indicating the changes in endogenous variables in response to a
change in each exogenous variable.

In this model, we ask two specific questions:
(1) Can we increase Y by an expansionary fiscal policy (an increase in G)?
(2) Can we increase Y by an expansionary monetary policy (an increase in Ms)?
G and Ms are the input variables and Y is the output variable
in question. (We may add that these questions themselves reflect the rather
old-fashioned mentality of macroeconomic fine-tuning. More recently, fiscal
and monetary policies are not considered as tools for adjusting real GDP.)
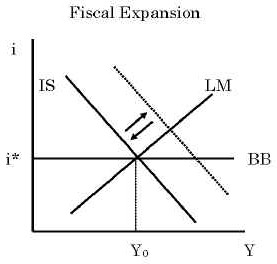
First, consider fiscal expansion.
1. An increase in G shifts the IS curve upward and to the right.
2. This puts an upward pressure on the domestic interest rate (i > i*).
3. But this immediately invites a massive capital inflow.
4. This appreciates the nominal exchange rate E as well as the real
exchange rate q.
5. This worsens the trade balance T.
As the model is constructed, no gradual adjustment is allowed; these events
are supposed to take place instantaneously. The exchange rate appreciates
and the trade balance worsens until the initial increase in G is completely
offset. The IS curve is pushed back to the original position, and Y cannot
increase at all.
What happened is that, in Y = A + T, as A is increased by fiscal
spending, T is reduced by exactly the same amount. Y is unchanged, and only
the relative composition of Y is changed. The conclusion is that under a floating
exchange rate and perfect capital mobility, fiscal policy is ineffective.
Here, "ineffective" means unable to increase Y.
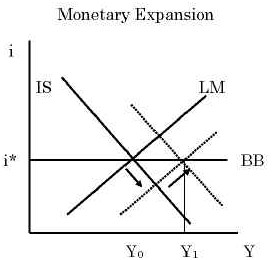
Second, consider monetary expansion.
1. An increase in Ms shifts the LM curve downward and to the
right.
2. This puts a downward pressure on the domestic interest rate (i < i*).
3. But this immediately invites a massive capital outflow.
4. This depreciates the nominal exchange rate E as well as the real
exchange rate q.
5. This improves the trade balance T.
Again, the whole sequence is assumed to take place in an instant.
Compared with the domestic version of IS-LM, monetary policy is more
powerful because the outward shift of LM invites an additional outward shift
of IS. Both LM and IS cooperate to increase income. The conclusion is that under a floating exchange rate and perfect capital
mobility, monetary policy is very effective.
These conclusions are significantly different from those of the domestic version of
the IS-LM model. In the domestic version, fiscal and
monetary policies are both effective, and their relative effectiveness depends
on various elasticities and slopes. But in this case, one policy is utterly
impotent and the other policy is doubly potent. By now, you should clearly
see why (by what mechanism and assumptions) these conclusions are generated.
In the next lecture, we will examine the case where the exchange rate is
fixed. You will see that conclusions on the two policies are completely
reversed. The Mundell-Fleming model produces extreme results.
Once again, let us summarize the Mundell-Fleming assumptions:
--Free float [this assumption can be changed--see next lecture]
--Perfect capital mobility [this assumption can also be modified]
--There are under-utilized resources and there is no supply constraint
--The Marshall-Lerner condition is satisfied
--The price level is fixed (in particular, there is no exchange rate
pass-through)
--No dollarization (no currency substitution)
--Exchange rate expectation is static and/or there is no risk premium
--Foreign P*, Y*, i* are given
Make sure all (or almost all) of these assumptions are met
before applying this model to the real world.
The Dutch disease
[See pp.355-357 in the Rivera-Batiz book]
As an appendix to the Mundell-Fleming model, we would like to discuss the
Dutch disease. This is an important question for many developing and
transition countries, especially those which have a lot of natural resources,
or receive a large amount of ODA, FDI or remittances relative to GDP.
Question: are countries with rich natural resources (oil, minerals,
etc) more likely to industrialize?
It may seem that having a large amount of natural resources is a big advantage for
industrialization because the nation can earn more foreign currency for investment.
But history shows that this is not necessarily so. Japan, Korea, Taiwan,
Singapore, Hong Kong and other countries that succeeded in catching up have
relatively high population density and relatively few natural resources. On the
other hand, Saudi Arabia, Kuwait, Brunei, Bolivia, Nigeria and other countries richly
endowed with natural resources have not industrialized.
Some economists (Jeffrey Sachs, for example) even argue that having no natural
resources is better for industrialization. Perhaps it is human resources,
not natural resources, that count.
But why so? The Dutch disease hypothesis provides one possible
explanation.
In the 1960s, with fixed exchange rates under the Bretton Woods system,
the Netherlands discovered off-shore natural gas. As natural gas was
extracted, it increased domestic income and spending. Investment was
redirected toward the natural gas sector. Dutch wages and prices
began to rise gradually. The Dutch guilder became overvalued in real terms,
their industrial products became uncompetitive, and the manufacturing sector shrunk.
This phenomenon of de-industrialization in the presence of rich natural resources was called the Dutch disease. They
got natural gas but lost manufacturing.
In the late 1970s and early 80s, the UK experienced similar
de-industrialization under a floating exchange rate regime. They discovered
and exploited the North Sea oil fields. Since the global oil price was rising, the UK was expected to earn a great amount of foreign exchange in the
future. But even before these earnings were realized, the British pound
appreciated suddenly in both nominal and real terms. This damaged the
British manufacturing sector.
UK Experiences De-industrialization as Oil Production
Begins
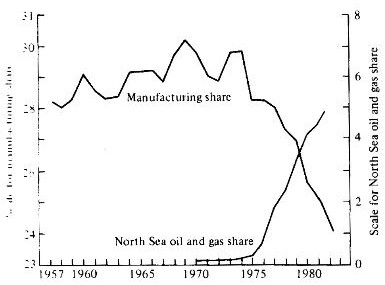
Source: F.L & L.A. Rivera-Batiz, International
Finance and Open Economy Macroeconomics (Optional Textbook), 2nd ed.,
1994, p.357. The left scale for manufacturing share and the right scale for
oil & gas share in GDP.
Definition; the Dutch disease is a situation where an expansion of the
natural resource sector leads to the shrinkage of other tradable industries
through overvaluation.
How overvaluation is generated depends on the exchange rate
regime. Under a fixed exchange rate, overvaluation occurs gradually
through rising domestic wages and prices. Under a floating exchange rate, overvaluation
is more abruptly caused by nominal exchange rate appreciation (often with
overshooting).
The Dutch disease is caused by a large injection of new purchasing power
into the economy. It occurs because domestic factors of production (labor,
capital) are limited while a new discovery creates an additional demand for
these factors. So some existing industries must shrink to make way. The Dutch
disease is most often associated with oil, gas and other minerals, because
they tend to be discovered suddenly and in large amounts. In theory, other
natural resource-based industries such as agriculture, forestry and fishery can also cause
the Dutch disease, but their output changes are usually not as dramatic as mineral
resources.
Moreover, a Dutch disease-like situation (overvaluation) can be generated with large
receipts of ODA, FDI or other capital inflows. If you receive too much
foreign exchange, the exchange rate may stay too high even though domestic
products are expensive and uncompetitive.
Does this mean that having natural resources is a bad thing? Not
necessarily. Natural resources do serve as a shock absorber and a precious
earner of foreign exchange (provided that these earnings are wisely spent). But countries
with a lot of natural resources must conduct economic policies in a
different way than other countries. For example:
--If you rely heavily on a small number of natural resources, you are more
likely to be hit by global price and demand volatility. You should try to
diversify the export base.
--You should also save extra earnings for the rainy day. A special fund
for this purpose is useful. Extra earnings should be saved when the
price is high, and this saving should be used for investment when the price
is low (smoothed spending). Do not invest too much and spend all
earnings when the price is high.
--Use fiscal, monetary and exchange rate policies wisely to soften the
negative shocks to the manufacturing sector, so it does not have to shrink.
--Build a mechanism where natural resource revenues are directed toward
productive investment. Make sure the money is not siphoned off
politically.
--Have a comprehensive and long-term development plan, while
preparing for possible shocks. Know how to respond to them.
--Consider well whether the resources should be exported in raw form, or
they should be processed domestically to add value. One of the key
issues is whether domestic processing is internationally competitive in
terms of cost. If domestic processing is cost effective, its development
will promote employment and industrialization. But don't invest in it if the
cost is high; you will waste a large amount of national income.
<References>
Corden, Max, "Booming Sector and Dutch Disease Economics,"Oxford
Economic Papers 36, 1984, pp. 359-380.
Fleming, J.M., "Domestic Financial Policies under Fixed
and under Floating Exchange Rates," IMF Staff Papers, November
1962.
Mundel, Robert, "Capital Mobility and Stabilization Policy under Fixed
and Flexible Exchange Rates," Canadian Journal of Economics and
Political Science, November 1963.
 In
1963 when he was young, Prof.
Robert Mundell (photo) was working with Marcus Fleming at the IMF and
wrote a paper which gave birth to this model. He has been at Columbia University
(New York) in the last 25 years. He has been a strong advocate of stabilization of
major currencies and establishment of euro. In 1999, he won the Nobel Prize
in economics, partly because of the Mundell-Fleming model.
In
1963 when he was young, Prof.
Robert Mundell (photo) was working with Marcus Fleming at the IMF and
wrote a paper which gave birth to this model. He has been at Columbia University
(New York) in the last 25 years. He has been a strong advocate of stabilization of
major currencies and establishment of euro. In 1999, he won the Nobel Prize
in economics, partly because of the Mundell-Fleming model.






