(See handout no.4; chapters 4 & 5)
In international economics, key macroeconomic variables include the following (symbols are in parentheses; * means a foreign variable):
Exchange rate (e)
Prices (p, p*)
Interest rates (i, i*)
Current account (CA)
Capital account (KA)
GDP (y, y*)
How these variables are related is the central question of open macroeconomics. In this lecture, interest parities, or the relationships between the exchange rate (e) and interest rates (i, i*), are investigated. Please note that the arguments presented below are valid only among countries whose financial sectors are sufficiently developed and externally open. If a country is financially closed or its financial sector lacks depth, liquidity and institutional development (for example, without well-functioning spot and forward currency markets), interest parities do not hold.
There are two versions of interest parities: covered and uncovered. The covered version involves no exchange risks, while the uncovered version entails such risks and elements of speculation. Both interest parities (especially the uncovered version) are key building blocks of many open macroeconomic models.
In the next lecture, purchasing power parity (PPP), namely the relationship between the exchange rate (e) and prices (p, p*), will be discussed. That is also a key input to open macroeconomic modeling. This lecture will also make references to it.
Interest parities (as well as PPP presented in the next lecture) are a type of the law of one price in an integrated world. The law of one price says that identical commodities (or anything) bought and sold in different markets should bear the same price. Otherwise, there will be a profit opportunity in buying the commodity in one market and selling it in the other, and someone will surely do it (this activity of pursuing gain by combined purchase and sale, without changing the physical characteristics of the commodity, is called arbitrage). In an integrated and properly functioning market, arbitrage will surely continue until the law of one price is established, eliminating any further opportunity for excess profit. Then the two markets are really one.
Some markets show LOOP, but others do not. Whether they do or do not depends on (i) the characteristics of the merchandise (especially the transportation cost; heavy and bulky items are difficult to arbitrage); (ii) the characteristics of market competition and strategies of traders; and (iii) policy intervention (e.g., capital control, tax and tariff policies and other regulatory measures to artificially increase transaction costs or even entirely ban such trade).
If you are checking the prices of digital cameras or DVD players in different outlets in the electronic town of Akihabara, Tokyo, you are also a potential arbitrager. You will soon realize that the same models bear almost exactly the same price, namely LOOP holds quite firmly in Akihabara. A shuttle trader, or an individual who carries merchandise, say, from China to Kyrgyzstan, is also engaged in arbitrage. In this case, however, LOOP probably does not hold exactly due to uncertainty and transportation cost. Sellers may overcharge without the buyer knowing it. Integrated global financial markets also exhibits LOOP, and their arbitrage is extremely fast and tight.
In the case of interest parities, what are equalized are the rates of return across various interest-bearing financial instruments (bank deposits, bonds, bills, etc). Under free capital mobility, LOOP holds firmly and trivially for covered interest parity, but the validity of LOOP for uncovered interest parity is empirically very questionable. The difference is explained by the absence or presence of exchange risk (see below).
In order for interest parities to hold, the following assumptions are required.
(1) Free capital mobility--there is no official hindrance to arbitrage across countries.
(2) No transaction cost--there is no natural (market) hindrance to arbitrage across countries. Transaction is without charge or carries only a negligible charge.
(3) No default risk--financial investment is safe against business defaults, country risks, etc.
The above are necessary conditions for covered interest parity. There are no exchange, default or other risks related to financial investment. We are assuming a perfectly safe, risk-free world.
In the case of uncovered interest parity, the following assumption is added.
(4) Risk neutrality--investors care only about the long-run average return and do not care about the outcome of each investment.
Here, exchange risk is present although all other risks of financial investment are still assumed away. Investors are assumed to be neutral against this risk. That means they care only about the average results. Whether the variance (volatility) of the return of each investment is large or small does not concern them.
Covered and uncovered interest parities should not be confused with each other. They refer to two completely different situations.
When people and firms are permitted to buy and sell foreign assets, they can hold various exchange "positions," which are net holding balances in foreign currency. The positions are classified below.
|
Position |
Balance sheet situation | If home currency depreciates | If home currency appreciates | |
| "Open" | "Long" | Foreign assets > foreign liabilities | Gain | Loss |
| "Short" | Foreign assets < foreign liabilities | Loss | Gain | |
| "Square" | Foreign assets = foreign liabilities | No impact | ||
For example, suppose you have foreign securities worth $500 but have also borrowed $700 from the bank.. This means that you have the short position of $200. For simplicity, we assume all foreign assets and liabilities are denominated in USD. This allows us to concentrate on the movement of the domestic currency against USD, without worrying about the fluctuations among major currencies.
Suppose you are a manufacturer of a certain product and also engaged in foreign trade. As you conduct your daily transactions of buying foreign parts or exporting finished products to foreign markets, the exchange position naturally fluctuates and does not remain "square." This means that you may incur gain or loss depending on the exchange rate movement at any moment, which is often hard to predict. Suppose also that your main business is manufacturing and you are not interested in foreign currency speculation. Particularly, you want to avoid exchange losses.
If your country has sufficiently developed and externally open financial markets, there are two alternative ways to "cover" or "hedge"--i.e., make your exchange position square and avoid exchange risk (see handout no.4). More concretely, assume that you are a Japanese exporter of an industrial product expecting a receipt of $100 after 3 months. You want to fix this receipt in terms of yen (domestic currency) now. Suppose also that:
| S (spot exchange rate) is currently $1=100 yen |
| F (3-month forward exchange rate) is--initially--$1=102 yen |
| i (Japanese interest rate) is 4%/year |
| i* (US interest rate) is 6%/year |
The first method is forward cover. You go to a bank and make a forward contract today. That is to say, you agree to sell $100 to the bank after 3 months and receive a specified amount of yen (10,200 yen = $100 x 102) at that time. Then you wait for 3 months before executing this transaction. The exchange rate for selling USD in the future (forward rate, 102), offered by the bank, is different from the exchange rate for today (spot rate, 100).
The second method is borrow dollar and sell spot now. That is to say, you go to a bank and borrow $98.52 today, immediately convert it to yen (9,852yen) in the spot market and deposit it at the bank. After 3 months, you withdraw 9,951 yen (principal plus accrued interest) and simultaneously repay $100 (principal plus accrued interest) to the bank with the export receipt.
Either way, you fix the yen receipt as of today so there is no exchange risk. But with the assumptions illustrated above, forward cover yields 10,200 yen and the borrowing method yields only 9,951 yen. Clearly, everyone prefers the first method. That means that the situation is not in equilibrium.
If everyone tries to sell USD forward while no one buys USD forward, there will be an oversupply of forward dollar and its price will fall. It will fall until forward USD becomes precisely $1=99.51 yen; because at this rate, the first and second method will be equivalent. This is an example of financial arbitrage and LOOP. The same "commodity" (export receipt after three months' wait) obtained through the forward exchange market and the bank loan market now bears the same price. Needless to say, actual interest arbitrage occurs instantaneously, not sequentially and slowly.
The CIP condition can be written as follows:
(F-S)/S = (i-i*)/(1+i*)
or approximately,
(F-S)/S = i - i*
if i* is sufficiently small. This means that
F>S if and only if i > i*
F<S if and
only if i < i*
In words, if the domestic interest rate is higher than the foreign interest rate, the forward exchange rate (future dollar) must be higher than the spot exchange rate (today's dollar), and vice versa. This relationship should always hold among high-quality, low-risk financial instruments under capital mobility.
CIP can be used as a test for capital mobility. Sometimes the government says capital movement is liberalized but actual transactions are secretly controlled. If CIP holds, we can say that the country truly has an open capital market. The UK liberalized its capital market externally in 1979. Thereafter, CIP began to hold (see p.122 of Batiz-Batiz). Japan revised its foreign exchange law in December 1980, and CIP began to hold after that. Since then, CIP has always held between Japan and the US (handout no.4).
Since virtually all developed countries in North America, EU and Japan have open capital markets, CIP holds trivially and as a matter of course among key currencies of dollar, euro and yen--it would be surprising if the situation is otherwise (but not between Russia and China). You can check this with financial news reports on any day. The following is the data for April 18, 2002 as published in Nihon Keizai Shimbun (Japan Economic Journal, or Nikkei for short), the most influential Japanese economic newspaper:
|
CIP between Japan and the US (April
18, 2002) |
|
| Bilateral interest rate differential, (i - i*) | -1.7375% |
| Japanese interest rate, i (CD 3-month) | i = 0.0825% |
| American interest rate, i* (CD 3-month) | i* = 1.82% |
| Forward premium/discount on the dollar, (F-S)/S | -1.86% |
|
Gap between (i - i*) and (F-S)/S |
0.1225% |
While there is a small gap between the interest rate differential and the forward discount, the magnitude is fairly small. Even if CIP is holding, statistical discrepancy can arise from various reasons: (i) time difference between Tokyo and NY markets (data are not taken exactly at the same moment); (ii) Japanese and US certificate of deposits (CDs) are not perfectly substitutable due to different liquidity, tax rules, regulations, etc; and (iii) transaction costs.
There are a few additional remarks on CIP:
(1) Don't try to perform CIP yourself. Arbitrage for CIP is automatic and instantaneous. Leave it to banks and financial companies.(2) While causality is often mutual in economics, we can say that, for CIP, main causality runs from the interest rate gap to the forward exchange rate. In other words, F is determined by the difference between i and i*.
(3) Some exchange risks cannot be hedged (or covered). Unhedgeable exchange risks include the following:
(i) Protection against a high or low exchange rate level, in contrast to protection against change from now to future. No banks will help you even if you complain about the current exchange rate level.
(ii) Long-term exchange risks. Usually, forward markets beyond 1 year are either nonexistent or extremely thin.
(iii) Business risks which are inseparable from exchange risk. If you are a manufacturing firm, your business carries many risks other than the exchange risk. You don't know whether your factories will operate smoothly without technical or labor troubles, whether the market will grow, and whether you can beat other competitors. Because these business uncertainties always exist, you don't know what exchange positions you will have next month, next year, or beyond. But if you don't know them, you can't go to the bank and hedge them! While fancy financial instruments like futures, options and swaps are available, exchange risk cannot be eliminated but must be added to the existing business risks. Technically speaking, this problem arises from the incompleteness of forward commodity contracts. Ronald McKinnon calls this the Arrow-Debreu dilemma.
UIP is very different from CIP. It involves exchange risk and speculation. In reality, UIP may or may not hold due to the existence of this uncertainty. Indeed, the bulk of empirical evidence suggests that it usually does not hold. Nevertheless, economists still use UIP because it is so convenient in model building.
The idea of UIP is very simple. You have two options in financial investment:
First option--purchase a domestic bond. Its return (in terms of domestic currency) is i.Second option--purchase a foreign bond. Its return (in terms of domestic currency) is i* + x.
x is the expected change in the exchange rate from now to future. i and i* are certain but x is uncertain. While the first investment yields a certain return, the second does not (from the viewpoint of accounting based on the domestic currency).
If you are risk-neutral (care only about the average return over many occasions instead of actual outcome this time), the LOOP condition for UIP is simply i = i* + x, or
x = i - i*
In words, the expected change in the exchange rate is equal to the bilateral interest rate gap. Note that, if both CIP and UIP hold simultaneously, we have x = (F-S)/S: that is to say, exchange rate expectation is equivalent to the forward premium.
Three remarks are in order:
(1) Exchange rate expectations are generally unobservable, but for some special cases, survey data are available from financial service companies or organizations such as IMM or JCIF (often at a substantial cost and/or with proper connections). The survey typically reports the expectations of traders, brokers, banks, financial companies, etc. for 1, 3 or 6 months ahead. According to studies using these surveys, short-term expectations are often divergent (the current movement is assumed to continue) while long-term expectations are regressive. In plain English, market participants think that the current unusual movement is temporary and the exchange rate will later return to the original level. Furthermore, there is a large divergence of opinion among experts. Such divergence increases especially at the time of financial turbulence.(2) UIP can be decomposed into three parts: (i) purchasing power parity (PPP: see next lecture); (ii) the Fisher equation regarding the relationship between nominal and real interest rates; and (iii) free capital mobility in terms of equalized real interest rates. We know that (i) does not hold in the short run. The empirical validity of the other two is also suspect (handout no.4).
(3) Investors may be risk-averse rather than risk-neutral as assumed here. In other words, they worry about both the average return of their investment and the degree of certainty (or variance) of that return. To be induced to invest in a risky asset, they require a higher average return to compensate for increased uncertainty. In this case, the UIP condition can be modified thus:
x = i - i* - z
Now we are comparing the two returns, i for the domestic bond and (i* + x + z) for the foreign bond. The risk premium z becomes necessary since investing in the foreign asset is risky. More precisely, the sign and the size of risk premium depend on (i) the degree of investors' risk aversion; and (ii) the relative supply of domestic and foreign assets that the investor community is collectively holding, which in turn depends on the cumulative current account surpluses or deficits of the two countries concerned.
Although its empirical validity is questionable, UIP is a very useful tool for macroeconomic model building. For example, the following famous models use UIP as a key component. These models are introduced for illustrations only and equations are reduced to bare minimum to explain the basic working of the models. The original formulations contain more variables and relations.
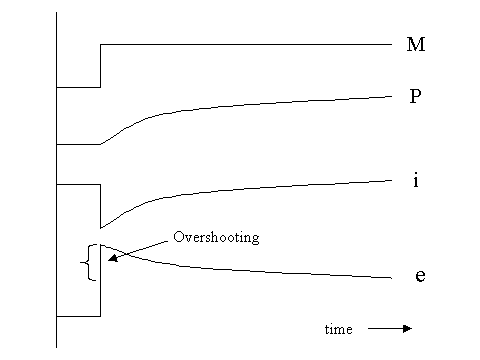
(1) Dornbusch overshooting exchange rate model
LM : M/P = L (i, y) (y is assumed fixed for simplicity)
UIP: x = i - i* (i* is assumed fixed for simplicity)
Prices are sticky (that is, P can move gradually but cannot jump instantaneously)
"Overshooting" here refers to the behavior of an exchange rate that swings beyond the long-term equilibrium level before coming back to it.
The Dornbusch overshooting model explains why the exchange rate is so volatile in a financially integrated world. The overshooting is generated essentially by the LM curve, UIP and sticky price. In this model, the IS curve is not essential for generating overshooting and needed only to close the model.
Suppose M (money supply) unexpectedly rises. Since P and y cannot jump, the LM curve says that i must go down immediately to balance the money market. According to UIP, this forces x to go down also (expectation of future appreciation of the domestic currency). Separately, in the long run, P and e (exchange rate) must rise proportionately to the rise in M (assuming monetarism and PPP). How can we have an expectation of future appreciation and still manage to depreciate e in the long run? By depreciating a large amount at the initial moment, so e can appreciate later ! This is the essence of the Dornbusch overshooting model.

(2) Portfolio-balance model
UIP: x = i - i* - z (z is risk premium, which is optional)
Expected exchange rate change: x = (p - p*) + k (PPP - e)
where p is inflation, PPP is purchasing power parity exchange rate, and k is the adjustment speed (k>0).
This is one of the most popular theoretical models of exchange rate determination. The second equation says that the expected movement of the exchange rate x has two components: (i) p- p* which is PPP in the change form; and (ii) the slow return of the actual rate to PPP. Risk aversion (pink addition) can be introduced to this model without changing its main characteristics.
The two equations can be combined to give:
e = PPP + (1/k) (r* - r) + (z/k)
where r is the real exchange rate (= i - p). This says that the actual exchange rate is a combination of the following components: (i) PPP; (ii) real interest differential; and (iii) optional risk premium.
(3) First generation model of currency crisis
The following equations, in log-linear form, are adopted from Robert Flood and Nancy Marion with minor change in symbols.
LM : m - p = - a(i)
where a is a positive scalar;
income (y) is ignored for simplicityDefinition of money supply:
m = d + r
where d is domestic credit;
r is international reservesPPP: p = p* + e (Note: p here is log of price, not its change)
UIP: x = i - i*
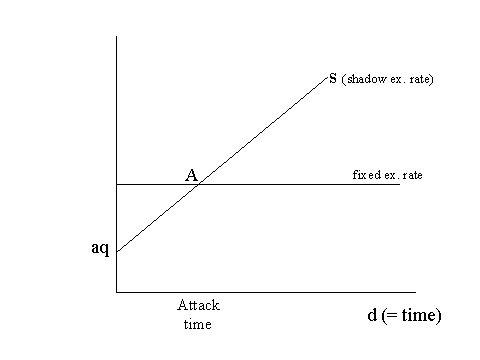
It is assumed that the government fixes e and simultaneously increases d at a constant rate q, to finance budget deficits. Even under the fixed exchange rate system, we can calculate a hypothetical exchange rate s (shadow exchange rate) which would prevail if speculators suddenly attack the domestic currency, international reserves are depleted, and the country switches to floating:
Shadow exchange rate: s = aq + d
Since the government continues to print money while fixing the exchange rate, the situation is fundamentally unsustainable. The question is: when do speculators attack? The answer is, when d is sufficiently expanded so that the actual fixed rate and the shadow exchange rate are the same. In the diagram below, A is such a point. To the left of A, the domestic currency will appreciate immediately after the attack and speculators will lose money, so no one will attack. To the right of A, the domestic currency will depreciate and speculators will make money, so everyone will attack. Competition among speculators (arbitrage !) will make sure that the actual attack will occur at the point where there will be no jump in the exchange rate.
[To be sure, the original models are highly complex and explanations given here are rather terse. My intention is to convey the sense of how UIP is incorporated in these models as a crucial element without going into technical details. Don't worry too much if you don't fully understand the models.]
<References>
Dornbusch, Rudiger, "Expectations and Exchange Rate Dyanmics," Journal of Political Economy 84, pp.1161-76, 1976.
Dornbusch, Rudiger, Open Economy Macro-economics, chapter 11, Basic Books, 1980.
Dornbusch, Rudiger, Exchange Rates and Inflation, MIT Press, 1988.
Flood, Robert, and Nancy Marion, "Perspectives on the Recent Currency Crisis Literature," NBER Working Paper no. 6380, January 1998.